| Finite-Elemente-Methode | ||
Finite-Elemente-Methode (FEM). Verfahren zur numerischen Lösung der verschiedensten Aufgaben aus dem Ingenieurbereich. Es findet u.a. Anwendung bei der Berechnung von Temperaturfeldern (Temperaturgradient), bei Strukturanalysen (Ermittlung von Spannungen und Verformungen) sowie bei der Untersuchung von Schwingungserscheinungen. Auch nichtlineare Effekte, wie z.B. Plastifizierungs- und Kriechvorgänge lassen sich mit Hilfe der FEM behandeln. Das Verfahren beruht auf einer Zerlegung des betrachteten Körpers in eine größere Anzahl endlicher Teile (finite Elemente), die über Knotenpunkte miteinander verknüpft sind. |
Durch Lösen eines linearen Gleichungssystems können dann die interessierenden Größen (z.B. Temperatur, Verschiebungen) für die Knotenpunkte ermittelt werden. Wegen der Komplexität des Gleichungssystems ist dazu eine leistungsfähige Rechenanlage erforderlich. Zur Auswertung der Ergebnisse stehen in der Regel umfangreiche graphische Möglichkeiten zur Verfügung (z.B. Farbdarstellung von Spannungen, Isolinien-und Verformungsbilder). |
|
| Verformungsplot vom Gleitring einer GLRD 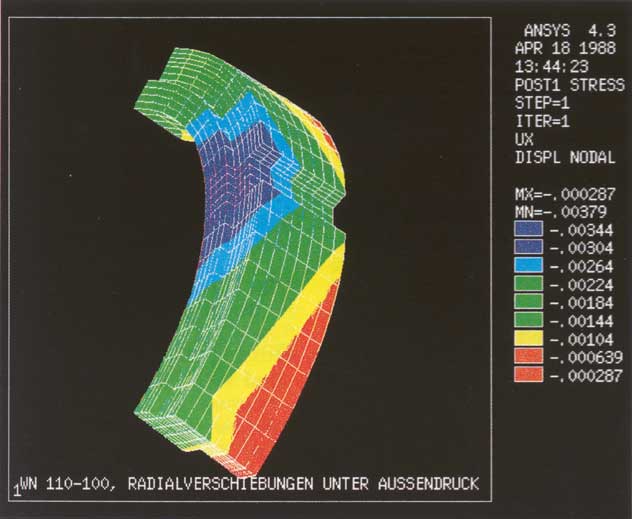
|
||